Simulated Annealing

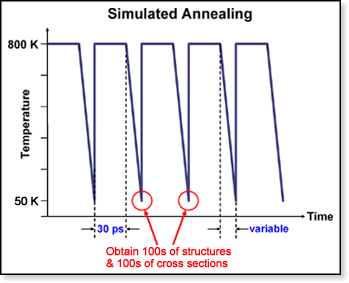    The simulated annealing procedure is used to generate a group of candidate molecular structures by molecular mechanics. The cross sections of these theoretical structures can then be compared with experimental results. (The method used for obtaining cross sections from theoretical molecular structures is detailed in the section on Theoretical Collision Cross Sections.) The structures are generated using the AMBER suite of programs by subjecting a starting conformation to 30 ps of dynamics at 800 K, then cooling it to 50 K over a variable period of time. From there, the molecule is geometry-optimized by minimizing its energy. This first candidate structure is then used as a new input conformation and subjected to the same annealing sequence. In this fashion typically 100 candidate structures are generated in an attempt to cover reasonable conformations for a given system. This procedure is illustrated in the figure above. The results of the annealing process are often presented as a scatter plot of cross section versus relative energy. An example of a scatter plot is shown below for the dinucleotide (dGC-H)^-. Each point represents a theoretical structure obtained in the simulated annealing process. The structures obtained in this process can often be grouped into families with similar structural features. Conformations within 5 kcal/mol of the lowest-energy conformation are generally considered reasonable models.
    The cooling step in the annealing protocol is an important one. The temperature drop has to occur sufficiently slowly to ensure appropriate equilibrium of the system. Since the equilibration time is temperature-dependant with rapid equilibration at high temperatures and slow equilibration at low temperatures, an exponential temperature profile is most suitable for locating the global minimum. However, in the past we have repeatedly found experimental evidence for the existence of structures other than the AMBER global minimum. Hence, locating reasonable theoretical structures above the global minimum is often useful for the interpretation of experimental data. Therefore, full equilibration during the cooling step is not always desired, and we found that a linear temperature profile from 800 K to 50 K does a reasonable job for our purposes (see "linear profile sampling procedure" below).
    The simulated annealing approach with a linear temperature profile during the cooling step has been evaluated using the oligoglycine system of small peptides. The method appears to cover conformational space fairly well for molecules of this size. Details of the evaluation are given below, but as an example, protonated pentaglycine was found to have 28 different conformers (out of 100 attempts) spread over an energy range of about 15 kcal/mol, 9 of them within the lowest 5 kcal/mol. Thus each conformation was found more than 3 times on average. However, the low-energy conformations were located much more frequently, for instance, the one with the lowest energy 25 times.

    Evaluation of the "linear profile sampling procedure". The simulated annealing procedure has been used in our group on a number of systems including crown ethers, oligosaccharides, synthetic polymers and peptides such as bradykinin. To gauge how well this method leads to the desired molecular structures, we have performed an in-depth analysis of the small peptide systems Gly_nH⁺ and Gly_nNa⁺ for n = 1-6. The concept of simulated annealing has clearly not been developed with the intention of covering the entire conformational space of a molecule, but rather as a means of searching for the global minimum on a potential energy surface. The method obviously discriminates against higher-energy conformers. Therefore, we do not expect to find all possible minima on the potential energy surface, but rather those deep wells that are sufficiently distant from the nearest deeper well and separated from it by a substantial barrier. It is the conformers associated with these minima in which we are most interested.
    For each of the systems Gly_nH⁺ (with protonated N-terminus), Gly_n(cs)Na⁺ (with Gly_n in a non-zwitterion charge solvation structure), and Gly_n(zw)Na⁺ (with a Gly_n zwitterion), one hundred low-energy conformers were determined using AMBER as described above. For each species investigated, some of the 100 conformers are identical. We are therefore interested in how many distinct conformations are found as well as whether the lowest-energy conformation is the one most frequently located. A table summarizing this type of data for the oligoglycine systems is shown below. The data show, not surprisingly, that the number of distinct conformers found increases with 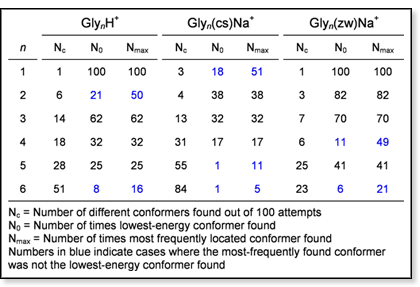increasing system size and that it approximately doubles for each additional glycine unit. In almost all cases, the lowest-energy conformation located was found more than five out of 100 attempts. The only exceptions are Gly₅(cs)Na⁺ and Gly₆(cs)Na⁺. In these cases, many slightly different conformers with very similar energies were found. In general, the lowest-energy conformer is also the one found most frequently. However, there are a few exceptions, indicating that not only the depth of a well, but also the size of the area in conformational space leading into the well is a determining factor for the probability of its detection. A striking example of this is the Gly₅(cs)Na⁺ system: while the lowest-energy conformation was found only once out of 100 structures, another more extended conformation with an energy ~1.5 kcal/mol above that of the lowest-energy conformation is located more than 10 times.
    It is important to consider whether the trends observed for these relatively small oligoglycine compounds will carry over to larger systems. The data in the table above suggests that a thorough search for the global minimum should include at least 100 annealing cycles for hexaglycine and should be doubled for each additional glycine unit. However, in many cases, the exact location of the global minimum is not required, but tracking down a local minimum near the global minimum is sufficient. We have to keep in mind that the potential energy surface itself is described by a rather crude model. Thus, the global minimum of the model is not necessarily expected to represent the true lowest-energy conformation anyway. Furthermore, one single zero-Kelvin structure is not a very useful comparison with any experimental data, usually obtained at T >> 0 K. Therefore a coarser search, cutting down computational effort by a factor of 2 to 10 from the guidelines given above, can be justified. If desired, the model global minimum could be found rapidly by an additional local search around the deepest local wells.