Experimental Collision Cross Sections

    The reduced mobility K₀ of an ion drifting through a buffer gas, discussed in the previous section, can be related to its collision cross section using kinetic theory.

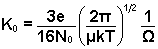
In this expression, e is the charge on the ion, N₀ the buffer gas number density at P₀ and T₀, μ the reduced mass of the buffer gas and ion, T the effective temperature, and the momentum transfer collision integral. Thus, by measuring K₀ we obtain a value for , an experimental "cross section".
    Kinetic theory indicates that the quantity is a momentum transfer collision integral. It is generally very difficult to calculate theoretically, unless it is calculated for a rigid sphere, in which case is equal to the projection cross section . For a general geometrical shape the projection cross section, which is fairly straight forward to calculate for any shape, is only an approximation for the collision integral.

However, for similar shapes, differences between and are similar and can be corrected for empirically. Differences between and are largest (up to 20%) for exotic geometries with large concave surfaces like bowls. (See e.g. Shvartsburg, A. A.; Jarrold, M. F. Chem. Phys. Lett. 1996, 261, 86-91 and Shvartsburg, A. A.; Schatz, G. C.; Jarrold, M. F. J. Chem. Phys. 1998, 108, 2416-2423.)

See also: "Theory/Analysis: Theoretical Collision Cross Sections"