|
Determination
of 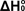 from from 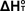 Using Statistical Mechanics
Using Statistical Mechanics
The
calculation of 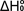 from from 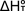 can be made using the following equation, where the integral is over the
different components of heat capacity: translational, rotational and vibrational
(as well as electronic is some cases).
can be made using the following equation, where the integral is over the
different components of heat capacity: translational, rotational and vibrational
(as well as electronic is some cases).

However,
we routinely use a somewhat more sophisticated method whereby 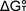 is calculated as a function of temperature for direct comparison with
our experimental data. In this approach, the various contributions to
the entropy must also be included, as shown below and
is calculated as a function of temperature for direct comparison with
our experimental data. In this approach, the various contributions to
the entropy must also be included, as shown below and 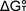 is then calculated as
is then calculated as 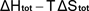 . .
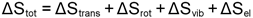
A
typical plot of experimental 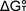 vs. T is shown below along with the calculated fit. The difference
between the straight line through the data points and the calculated curve
at 0 K is exactly equal to the heat capacity correction given in the first
equation above. By performing the analysis in this way, the parameters
which affect the heat capacity corrections are tuned in order to reproduce
the experimental entropy (roughly equal to the slope of these
vs. T is shown below along with the calculated fit. The difference
between the straight line through the data points and the calculated curve
at 0 K is exactly equal to the heat capacity correction given in the first
equation above. By performing the analysis in this way, the parameters
which affect the heat capacity corrections are tuned in order to reproduce
the experimental entropy (roughly equal to the slope of these  vs. T plots).
vs. T plots).
Whether
an analysis is carried out by simply calculating the heat capacity corrections
or by modeling the entire  vs. T curve, one needs various molecular parameters. These include
the masses of the species involved (for translational terms), moments
of inertia (for rotational terms), and vibrational frequencies (for vibrational
terms). If there are low-lying excited electronic states that are thermally
accessible, their relative energies are also needed for the electronic
contribution. The masses are known - this is a mass-spectrometry-based
method after all. Molecular modeling is usually used to determine the
rotational constants and frequencies. Rotational constants are relatively
easy to calculate from even a somewhat crude approximate structure. Vibrations
are more difficult to calculate, but contribute much less to the final
result. That is, the fitting procedure described here is relatively insensitive
to errors in vibrational frequencies, and only frequencies of less than
a few hundred wavenumbers contribute much to the heat capacity or entropy.
There is a further term included to compensate for any instrumental mass
discrimination that may exist. This accounts for any mass-dependent bias
in the transmission through the final mass-selection stage of the experiment.
Any mass discrimination, MD, will lead to an effective entropy
correction of R·ln(MD).* Therefore, a reasonable
set of parameters is chosen for a particular system, the fit to experiment
is performed by varying MD as well as
vs. T curve, one needs various molecular parameters. These include
the masses of the species involved (for translational terms), moments
of inertia (for rotational terms), and vibrational frequencies (for vibrational
terms). If there are low-lying excited electronic states that are thermally
accessible, their relative energies are also needed for the electronic
contribution. The masses are known - this is a mass-spectrometry-based
method after all. Molecular modeling is usually used to determine the
rotational constants and frequencies. Rotational constants are relatively
easy to calculate from even a somewhat crude approximate structure. Vibrations
are more difficult to calculate, but contribute much less to the final
result. That is, the fitting procedure described here is relatively insensitive
to errors in vibrational frequencies, and only frequencies of less than
a few hundred wavenumbers contribute much to the heat capacity or entropy.
There is a further term included to compensate for any instrumental mass
discrimination that may exist. This accounts for any mass-dependent bias
in the transmission through the final mass-selection stage of the experiment.
Any mass discrimination, MD, will lead to an effective entropy
correction of R·ln(MD).* Therefore, a reasonable
set of parameters is chosen for a particular system, the fit to experiment
is performed by varying MD as well as 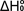 ,
and then the parameters are varied over a wide range (refitting MD
and ,
and then the parameters are varied over a wide range (refitting MD
and 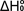 each time) to get the
resulting uncertainty in each time) to get the
resulting uncertainty in 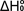 .
For species with low-lying excited electronic states, the electronic terms
are also added in, and differences in state multiplicities are also taken
into account. For cases where H2 is used as a buffer gas, the
full state counting approach to calculating the heat capacity and entropy
are included due to the very large rotational temperature of dihydrogen.
However, this is a rather small contribution to the final value of .
For species with low-lying excited electronic states, the electronic terms
are also added in, and differences in state multiplicities are also taken
into account. For cases where H2 is used as a buffer gas, the
full state counting approach to calculating the heat capacity and entropy
are included due to the very large rotational temperature of dihydrogen.
However, this is a rather small contribution to the final value of 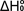 . .
It
is important to point out that, despite the seemingly large number of
parameters that can be varied (vibrational frequencies, rotational constants,
excited electronic state energies), this method gives well-determined
values of 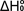 . Sufficiently
accurate values for the rotational constants are usually available from
ab initio or molecular dynamics calculations, depending on the size of
the system. Vibrational frequencies larger than a few hundred wavenumbers
have little effect on the heat capacity and entropy, so usually only a
small number of frequencies need to be varied. Also, excited electronic
states with energies a few kcal/mol above the ground state also have little
effect and such low-lying excited states are usually not present.
Inaccuracies in these parameters generally lead to errors in . Sufficiently
accurate values for the rotational constants are usually available from
ab initio or molecular dynamics calculations, depending on the size of
the system. Vibrational frequencies larger than a few hundred wavenumbers
have little effect on the heat capacity and entropy, so usually only a
small number of frequencies need to be varied. Also, excited electronic
states with energies a few kcal/mol above the ground state also have little
effect and such low-lying excited states are usually not present.
Inaccuracies in these parameters generally lead to errors in 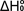 of a few tenths of a kcal/mol.
of a few tenths of a kcal/mol.
*MD is defined
as the ratio of transmission efficiency of product vs. reactant ions.
|

